flowchart LR
bbdd[("BBDD
urolitos")]
style bbdd color: #000000
3 Estadística descriptiva
Las dos grandes ramas de la estadística son la estadística descriptiva y la estadística inferencial. No son antagónicas ni mucho menos, sino más bien complementarias; de hecho, para realizar inferencias acertadas sobre un suceso es indispensable primero describir dicho suceso; por tanto, la estadística descriptiva es importante por sí sola y también como paso previo para realizar inferencias.
- Definición
Hay varias definiciones acerca de la estadística descripitva. A continuación se presentan algunas de ellas.
La estadística descriptiva se compone de aquellos métodos que incluyen técnicas para recolectar, presentar, analizar e interpretar datos.(Llinás and Rojas 2017)
La estadística descriptiva comprende un conjunto de métodos para organizar, resumir y presentar los datos de manera informativa.(Proaño 2020)
3.1 Distribución de frecuencias cualitativa
3.1.1 Teoría
Las frecuencias son en su origen básicamente conteos, y se refiere a qué tanto se repite un valor, dicho valor puede ser incluido en una categoría, así se forman las distribuciones de frecuencias, de acuerdo a (Martínez 2020) una distribución de frecuencias consiste en agrupar una serie de datos en varias clases o grupos que no se superponen.
Así como vimos que las variables pueden ser cuantitativas o cualitativas, las frecuencias también; es decir que se puede realizar una distribución de frecuencias tanto de variables cuantitativas como de variables cualitativas. Las frecuencias se pueden clasificar como frecuencias absolutas y frecuencias relativas.
Frecuencias absolutas
Las frecuencias absolutas no son más que los conteos brutos de determinada variable.
Frecuencias relativas
Las frecuencias relativas se construyen con la proporción de cada clase en relación al total de datos. Se calcula de la siguiente forma.
\[\begin{equation}{} Fr = \frac{F_i}{n} \end{equation}\]
Donde:
\(F_i = Frecuencia\phantom{0}absoluta\phantom{0}de\phantom{0}cada\phantom{0}clase\)
\(n = Número\phantom{0}total\phantom{0}de\phantom{0}datos\)
Los resultados obtenidos para cada clase son valores que están entre 0 y 1, la suma de las frecuencias relativas de todas las clases es igual a 1, si se quieren obtener las proporciones en porcentajes solo basta multiplicar el resultado por 100.
- Frecuencias porcentuales
Son frecuencias relativas pero en lugar de estar en un rango de 0 a 1 están en un rango de 0 a 100. Es decir que la proporción de cada clase respecto al total de datos está dada en porcentaje.
- Frecuencias acumulada
Las frecuencias acumuladas se pueden calcular tanto para frecuencias absolutas como relativas.
La frecuencia acumulada de una clase es la suma de las frecuencias para esa clase y todas las previas. (Triola 2004)
La frecuencia acumulada resulta útil en varias situaciones; por ejemplo, si se está evaluando un protocolo de atención al parto en cerdas, para ello se puede medir el tiempo entre el nacimiento de un lechón y otro. Se considera que el tiempo adecuado entre el nacimiento de un lechón y otro es de aproximadamente 15 minutos. Si una cerda tiene 10 lechones y su parto dura dos horas, su promedio es de un lechón nacido a cada doce minutos, esto puede parecer bueno; sin embargo, si la frecuencia acumulada fué muy incostante puede revelar algunos problemas; puede darse el caso en el que el parto no sea bien atendido y se den obstrucciones, en ese caso la frecuencia acumulada puede ser un indicador de que hubo distocia o un mal manejo en la atención del parto, si se nota que la frecuencia acumulada es incostante puede indagarse más y verificar si hubo un aumento en el número de lechones nacidos muertos porque entre otras cosas se puede presentar el síndrome de aspiración de meconio que de acuerdo a (Wiswell 1993) es un indicador de hipoxia.
3.1.2 Práctica
Supongamos que obtenemos datos de un hospital veterinario para la caracterización clínica de los casos de urolitiasis en perros que se presentaron a consulta en el año 2024.
Veamos la tabla original.
raza sexo edad
1 boxer macho adulto
2 labrador macho adulto
3 labrador macho adulto
4 bulldog hembra adulto
5 chihuahua hembra adulto
6 beagle hembra adulto
7 doberman macho adulto
8 doberman macho jóven
9 schnauzer hembra jóven
10 mestizo macho jóven
11 mestizo macho geriátrico
12 mestizo macho geriátricoUrolitiasis por raza
Frecuencia absoluta
Frecuencia relativa
Frecuencia porcentual
table(urolitos$raza);prop.table(table(urolitos$raza));prop.table(table(urolitos$raza))*100
beagle boxer bulldog chihuahua doberman labrador mestizo schnauzer
1 1 1 1 2 2 3 1
beagle boxer bulldog chihuahua doberman labrador mestizo
0.08333333 0.08333333 0.08333333 0.08333333 0.16666667 0.16666667 0.25000000
schnauzer
0.08333333
beagle boxer bulldog chihuahua doberman labrador mestizo schnauzer
8.333333 8.333333 8.333333 8.333333 16.666667 16.666667 25.000000 8.333333 Urolitias por sexo
Frecuencia absoluta
Frecuecnia relativa
Frecuencia porcentual
table(urolitos$sexo);prop.table(table(urolitos$sexo));prop.table(table(urolitos$sexo))*100
hembra macho
4 8
hembra macho
0.3333333 0.6666667
hembra macho
33.33333 66.66667 Urolitiasis por edad
Frecuencia absoluta
Frecuecnia relativa
Frecuencia porcentual
table(urolitos$edad);prop.table(table(urolitos$edad));prop.table(table(urolitos$edad))*100
adulto geriátrico jóven
7 2 3
adulto geriátrico jóven
0.5833333 0.1666667 0.2500000
adulto geriátrico jóven
58.33333 16.66667 25.00000 Estos resultados de urolitiasis en perros son coherentes con los encontrados por (Murales 2021) quien reporta una prevalencia de 57% en adultos, 28% en jóvenes y 15% en geriátricos.
Frecuencia acumulada
Se presentará la frecuencia acumulada para la variable edad
Frecuencia acumulada absoluta
cumsum(table(urolitos$edad))adulto geriátrico jóven 7 9 12Frecuencia acumulada relativa
cumsum(prop.table(table(urolitos$edad)))adulto geriátrico jóven 0.5833333 0.7500000 1.0000000Gráficas
Gráfica de barras
barplot(table(urolitos$sexo))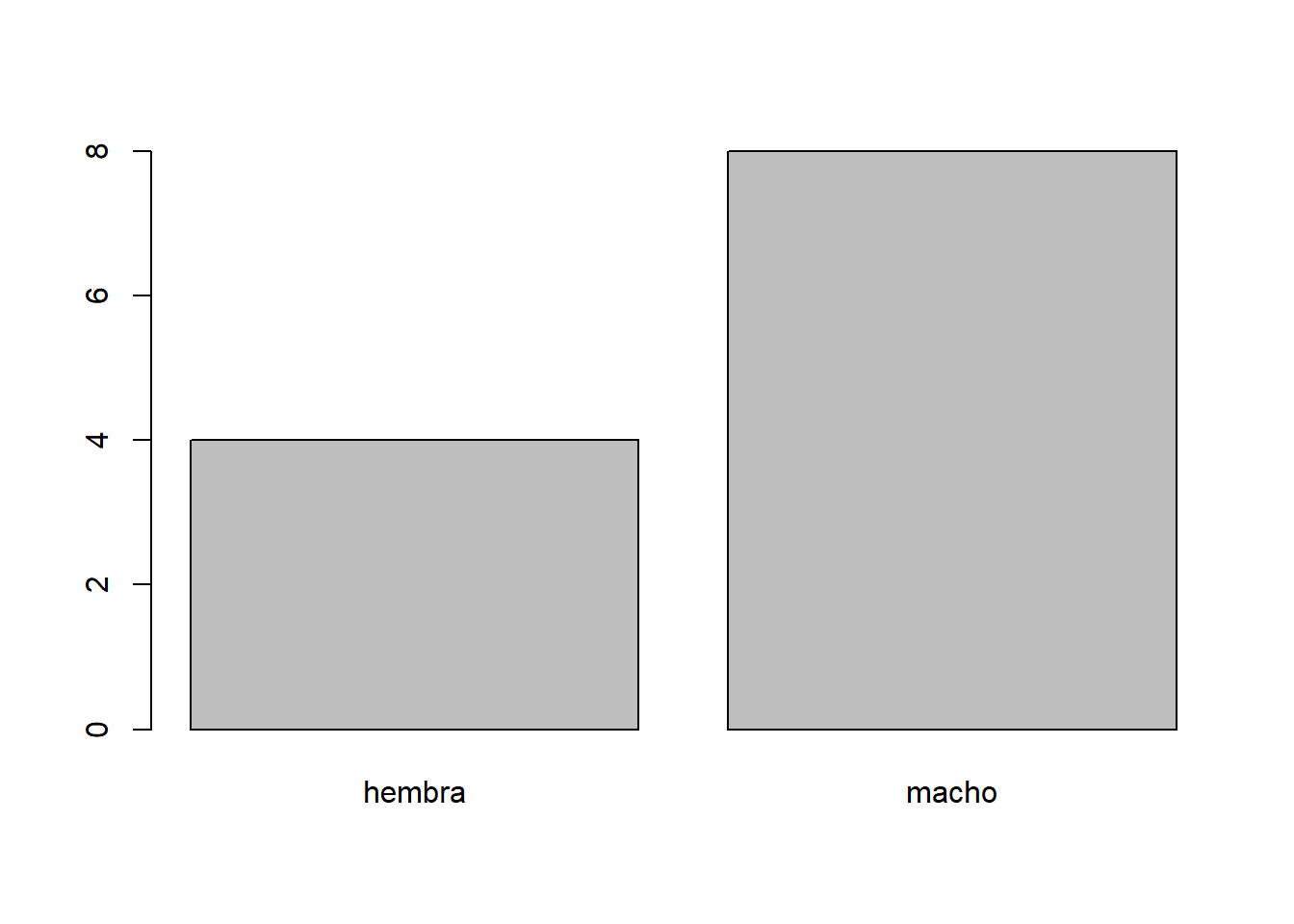
Gráfica de pastel
pie(table(urolitos$edad))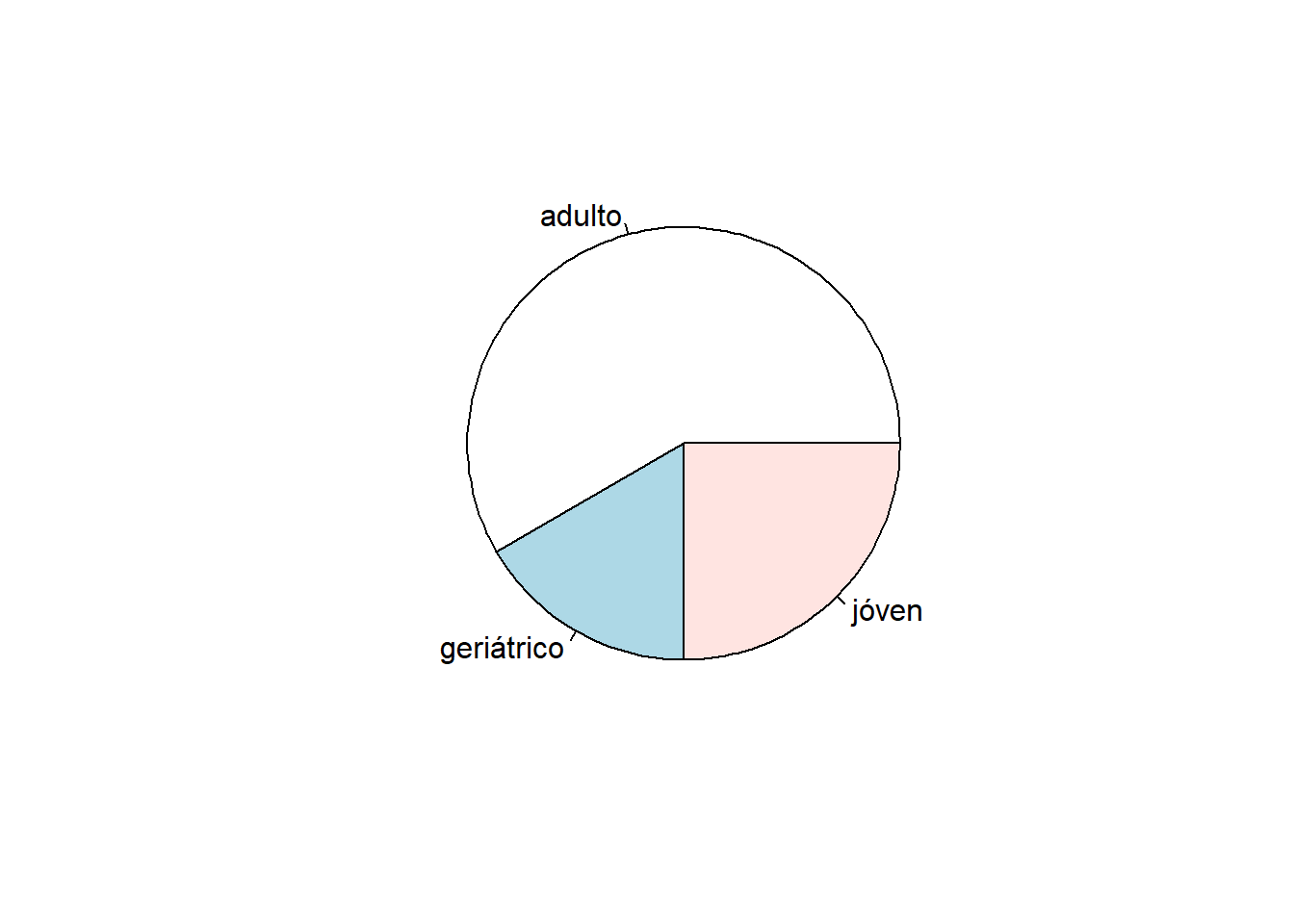
3.2 Distribución de frecuencias cuantitativa
3.2.1 Teoría
Una distribución de frecuencias es cuantitativa si se refiere a datos numéricos (Martínez 2020);
siendo más claros, una distribución de frecuencias cuantitativa se refiere a datos correspondientes a variables cuantitativas.
Para realizar una distribución de frecuencias cuantitativa se deben tener presente las siguientes definiciones
Rango
Es la diferencia entre el mayor y el menor de los datos. (Martínez 2020)
\[\begin{equation}{} R = Xmax - Xmin \end{equation}\]
Número de clases
Es la cantidad de clases que formará nuestra distribución, no debe ser un número tan grande ni tan pequeño, como regla general (Martínez 2020) suguiere que el número de clases esté comprendido entre 5 y 15, lo cuál está en concordancia con lo que suguiere (Sturges 1926) que indica que el número de clases más conveniente suelen ser cantidades como 1, 2, 5, 10, 15, 20, etc.
También el mismo (Sturges 1926) desarrolla una fórmula (que se muestra a continuación) para obtener la cantidad óptima de clases, y recomienda que el resultado de la fórmula sirva para que en la práctica se elija entre las cantidades convenientes (1, 2, 5, 10, 15, 20, etc.) la más cercana al resultado de la fórmula.
\[\begin{equation}{} NC = 1 + 3.32Log(N) \end{equation}\]
Donde
Log = Logaritmo de base 10
N = Número total de datos
Amplitud
También llamado amplitud de clase o anchura de clas. Es el resultado de dividir el rango dentro del número de clases.
\[\begin{equation}{} A = \frac{R}{NC} \end{equation}\]
Para aproximar el Vi siempre debe hacerse al entero superior.
Marca de clase
Las marcas de clase son cada uno de los promedios de los valores que componen cada clase, en la práctica se obtiene sumando el límite inferior y el superior de la clase y dividiéndolo dentro de 2.
3.2.2 Práctica
Se realizarán los pasos para crear la distribución de frecuencias utilizando datos que representan el peso de lechones destetados.
flowchart LR
bbdd[("BBDD
destete25")]
bbdd2[("BBDD
destete100")]
bbdd3[("BBDD
destete10000")]
style bbdd color: #000000
style bbdd2 color: #000000
style bbdd3 color: #000000
Rango
R <- max(destete25) - min(destete25) R[1] 11.9Número de clases
NC <- round(1 + 3.32 * log10(nrow(destete25)),0) NC[1] 6Valor del intervalo
A <- ceiling(R/NC) A[1] 2Límites
Li1 <- min(destete25) Li2 <- Li1+A Li3 <- Li2+A Li4 <- Li3+A Li5 <- Li4+A Li6 <- Li5+A Ls1 <- Li1 + A Ls2 <- Li2 + A Ls3 <- Li3 + A Ls4 <- Li4 + A Ls5 <- Li5 + A Ls6 <- Li6 + AMarca de clase
Mc1 <- (Li1 + Ls1) / 2 Mc2 <- (Li2 + Ls2) / 2 Mc3 <- (Li3 + Ls3) / 2 Mc4 <- (Li4 + Ls4) / 2 Mc5 <- (Li5 + Ls5) / 2 Mc6 <- (Li6 + Ls6) / 2Tabulación
tabla_frecuencias <-data.frame(
Li = c(Li1, Li2, Li3, Li4, Li5, Li6),
Ls = c(Ls1, Ls2, Ls3, Ls4, Ls5, Ls6),
Mc = c(Mc1, Mc2, Mc3, Mc4, Mc5, Mc6),
Frecuencia = c(1, 6, 9, 6, 2, 1)
)
tabla_frecuencias Li Ls Mc Frecuencia
1 3.9 5.9 4.9 1
2 5.9 7.9 6.9 6
3 7.9 9.9 8.9 9
4 9.9 11.9 10.9 6
5 11.9 13.9 12.9 2
6 13.9 15.9 14.9 1Dado que el límite superior de una clase es igual al límite inferior de la clase siguiente, cuando un valor sea exactamente igual a un límite deberá incluirse en la clase correspondiente al límite inferior; por ejemplo, si la clase 1 de una distribución tiene como límites 5 y 10 y la clase 2 tiene como límites 10 y 15 y se presenta el valor 10, este debe ser ubicado en la clase 1, de esta forma se evita duplicar valores.
Atajo
Con la función hist se pueden obtener de manera fácil los datos de la distribución de frecuencias.
Esta función es la utilizada para realizar gráficas de histograma, pero si le añadimos el argumento plot = F no se mostrará la gráfica y en su lugar se mostrará la información de la distribución de frecuencias
hist(destete25$peso, plot = F)$breaks [1] 2 4 6 8 10 12 14 16 $counts [1] 1 0 6 10 5 2 1 $density [1] 0.02 0.00 0.12 0.20 0.10 0.04 0.02 $mids [1] 3 5 7 9 11 13 15 $xname [1] "destete25$peso" $equidist [1] TRUE attr(,"class") [1] "histogram"Donde:
breaks = Límites
counts = Frecuencia de cada clase
density = Densidad de cada clase (frecuencia de clase (counts) / n * 2)
mids = Marca de clase
Nota: Los resultaos de los cálculos manuales pueden variar ligeramente en algunas ocasiones respecto a los resultados realizados con el atajo con el comando hist, sobre todo en el número de clases cuando n es muy grande, probablemente por la técnica de aproximación utilizada más que por fórmulas ya que el método que utiliza por defecto el comando hist para calcular el número de clases es el método Sturges el cuál es el mismo uilizado a mano.
Gráficas
Histograma:
Un histograma es la representación de frecuencias mediante rectángulos con base en el eje horizontal y altura proporcional a la frecuencia de las clases.
En el eje horizontal se colocarán las marcas de clase de cada una de las clases. (Martínez 2020)
Los histogramos se parecen mucho a los gráficos de barras; sin embargo, tienen diferencias sustanciales que hay qué reconocer, como bien indica (Celis and Labrada 2014) en los histogramas a diferencia de los gráficos de barras las columnas no se separan y la escala horizontal es cuantitativa.
Histograma con base de datos de 25 lechones
hist(destete25$peso)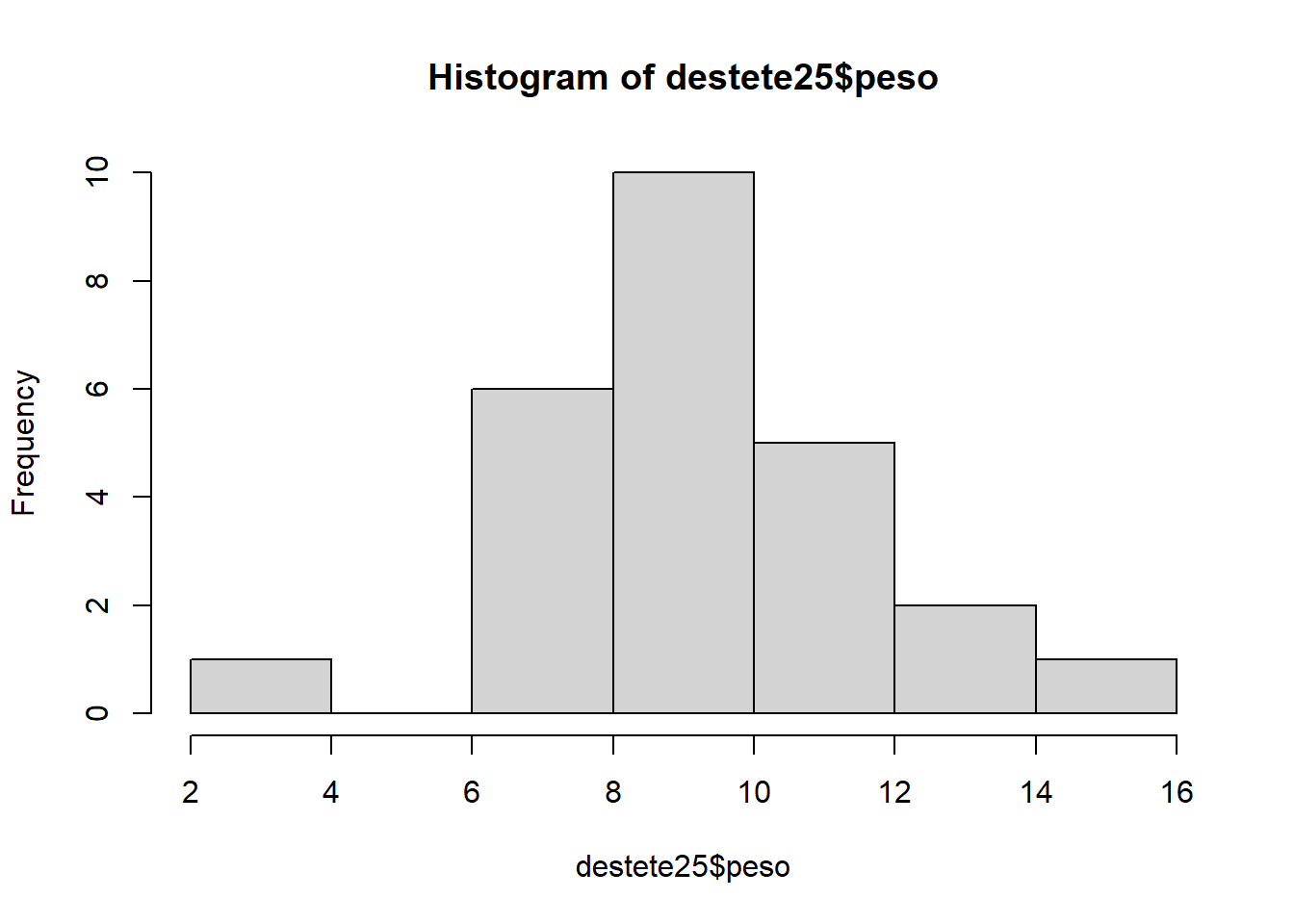
Histograma con base de datos de 100 lechones
hist(destete100$peso)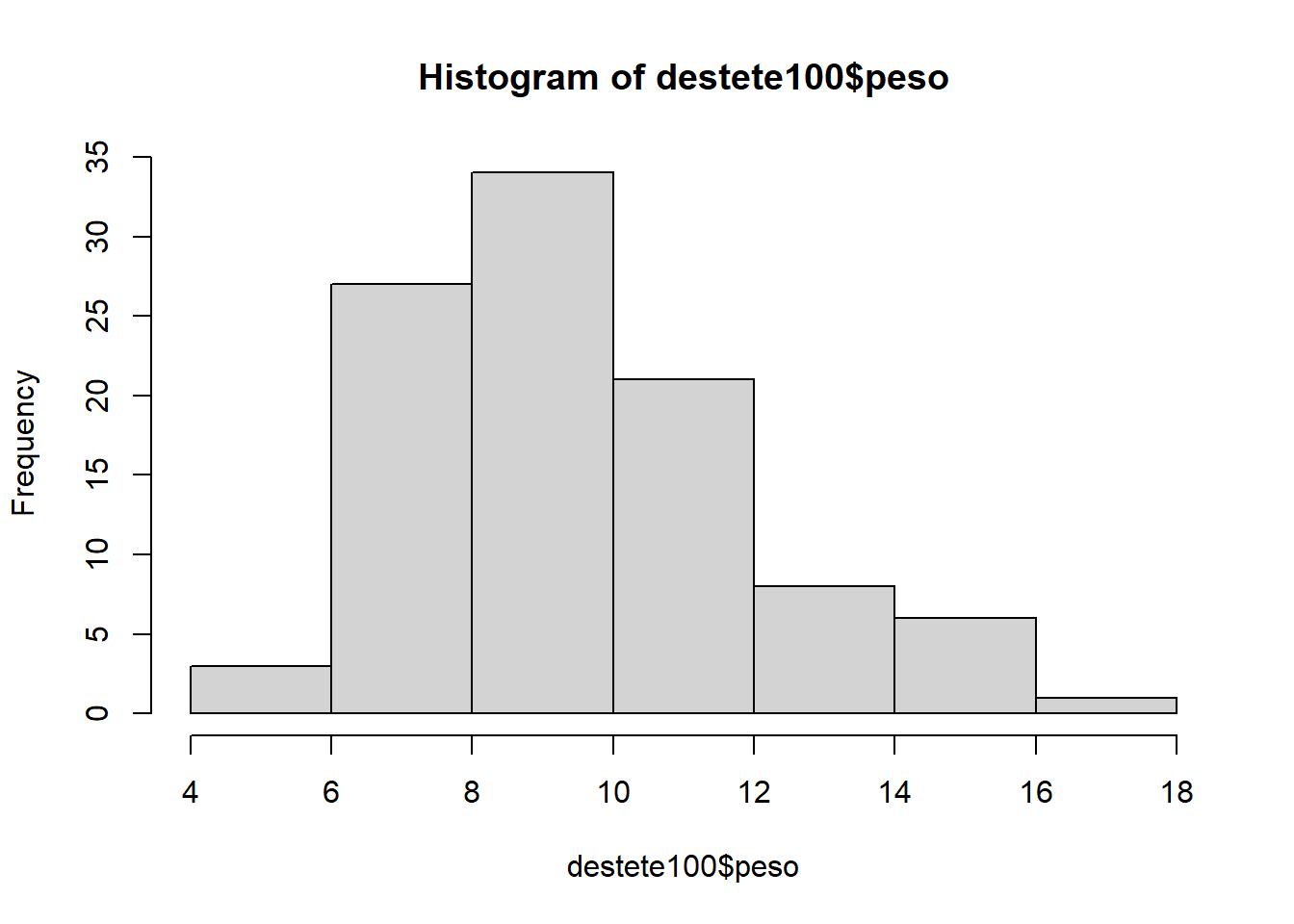
Histograma con base de datos de 10,000 lechones
hist(destete10000$peso)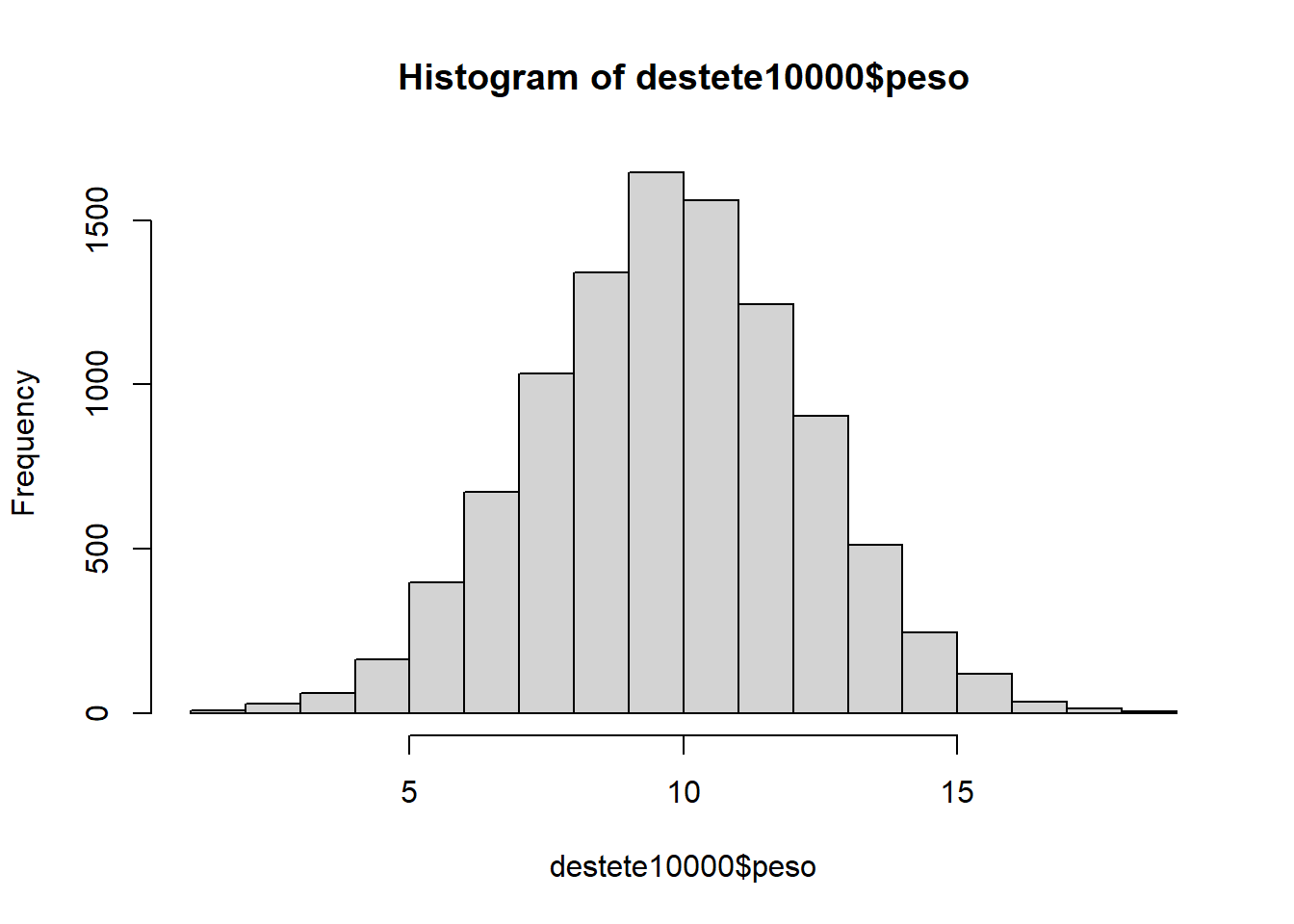
Ojiva:
Una ojiva es una gráfica lineal que representa frecuencias acumulativas, de la misma forma que la distribución de frecuencias acumulativas es una lista de éstas. (Triola 2004)
La ojiva se puede realizar a partir de las frecuencias absolutas, relativas, o porcentuales.
A continuación se mostrará una gráfica de ojiva a partir de las frecuencias absolutas
#Primero se calculan las frecuencias acumuladas
frecuencias_absolutas <- cumsum(hist(destete25$peso, plot = F)$counts)
#Luego se hace una gráfica de las frecuencias absolutas con el comando plot
plot(frecuencias_absolutas)
#Por último se grafican líneas sobre los puntos con el comando lines
lines(frecuencias_absolutas)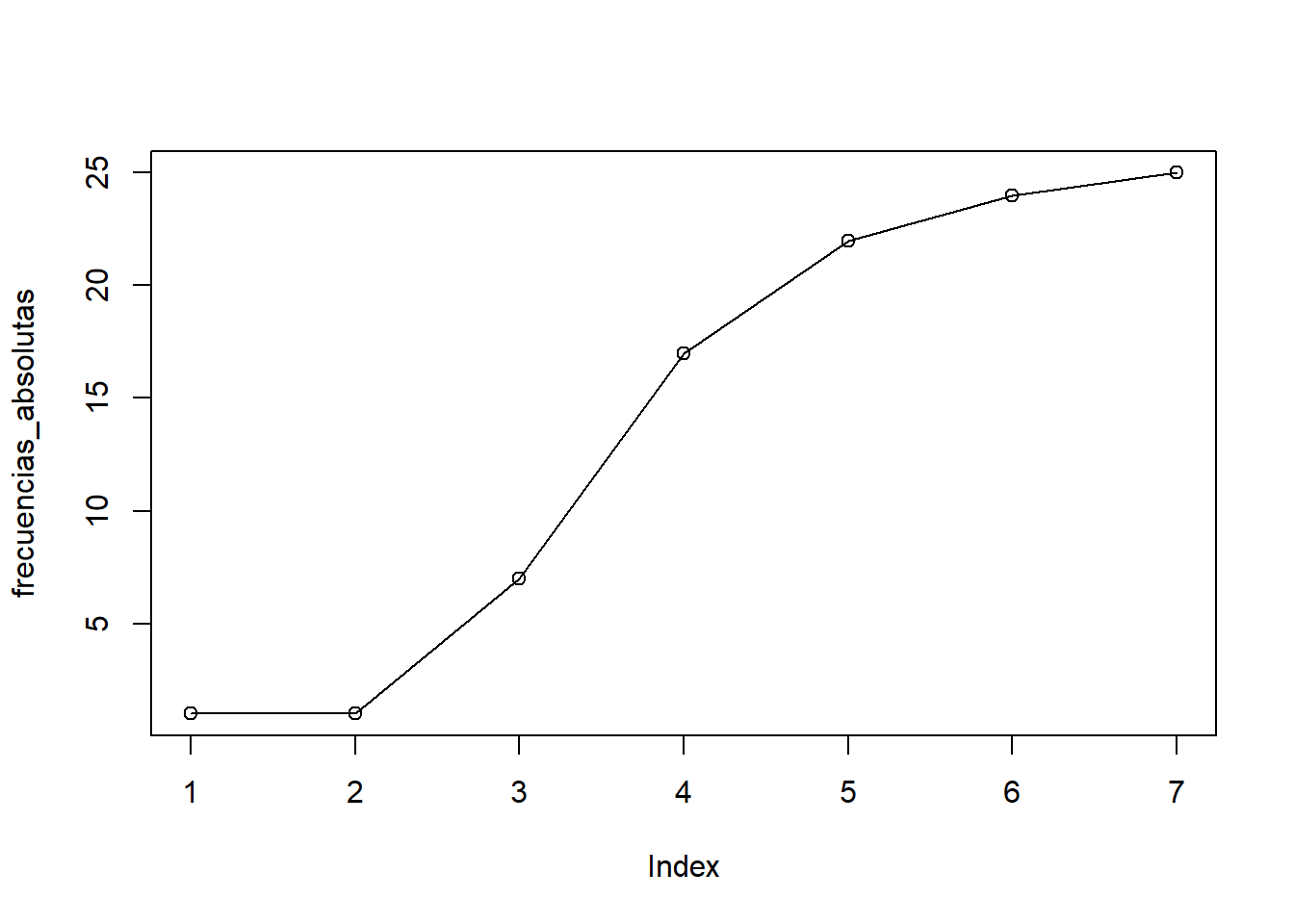
3.3 Medidas de tendencia central
3.3.1 Teoría
Una medida de tendencia central permite ubicar e identificar el punto alrededor del cuál se centran los datos.(Proaño 2020)
Las medidas de tendencia central más utilizadas son el promedio (o media aritmética), la mediana y la moda.
Promedio
El promedio es el punto de equilibro dentro de un conjunto de datos; como tal, no siempre estará justo a la mitad del conjunto de datos, pero siempre tiende a estar cerca del centro.
Cuando el promedio se extrae de una muestra, se dice que es un promedio muestral (osea, un estadístico), y se designa con el símbolo \(\bar{x}\), su fórmula es la siguiente
\[\begin{equation}{} \bar{x} = \frac{\sum_{i =1}^{n}{x_i}}{n} \end{equation}\]
Esta fórmula significa que se debe sumar cada valor x desde i = 1 hasta n, es decir que hay qué tomar cada valor del conjunto de datos desde el primer valor hasta el último de los valores de la muestra, luego se divide esa sumatoria dentro del total de datos (n).
Cuando el promedio se extrae de la población, se dice que es un promedio poblacional (osea un parámetro), y se designa con la letra griega “mu” (\(\mu\)), su fórmula es la siguiente
\[\begin{equation}{} \mu = \frac{\sum_{i =1}^{N}{x_i}}{N} \end{equation}\]
La única diferencia entre el promedio muestral y el poblacional es que en el promedio muestral se usa n (total de datos de la muestra) y en el promedio poblacional se usa N (total de datos de la población)
- Mediana
Implica el valor que está en medio, cuando los valores originales de los datos se presentan en orden de magnitud creciente (o decreciente).(Triola 2004) Algunas veces habrá un solo dato que está justo en medio del conjunto de valores; sin embargo, a veces habrán dos, por eso (Spiegel and Stephens 2009) nos indica que la mediana es el valor central o la media de los dos valores centrales.
Específicamente la mediana será justo el valor que está en el centro de los datos ordenados cuando el conjunto de datos sea par, mientras que la mediana será el promedio de los dos valores centrales cuando el conjunto de datos ea impar.
Dado que la mediana es a la vez una medida de tendencia central y a la vez es una medida de posición (porque se posiciona justo en el centro del conjunto de datos), para su cálculo primero hay qué determinar la posición en la que se separa el conjunto de datos en dos mitades (50% hacia arriba y 50% hacia abajo) y luego observar qué dato está en esa posición.
Se puede resumir el cálculo de la mediana en tres pasos:
Ordenar los datos: De preferencia ascendentemente.
Calcular la posición:
\[\begin{equation}{} Posición = \frac{n + 1}{2} \end{equation}\]
Hallar el valor correspondiente a la posición central:
Si el resultado de la posición es un número entero basta con buscar el valor que se encuentra en esa posición.
Si el resultado de la posición es número impar entonces hay qué calcular el promedio de los dos valores centrales.
Moda
La moda, como bien indica (Celis and Labrada 2014) es el valor que más se repite en un grupo de datos, y así como en un conjunto de datos puede haber más de una moda también puede suceder que no tenga moda.
3.3.2 Práctica
flowchart LR
bbdd[("BBDD
destete25")]
style bbdd color: #000000
- Promedio
mean(destete25$peso)[1] 9.1552- Mediana
median(destete25$peso)[1] 8.53- Moda
Hay varias formas distintas de calcular la moda, ahora veremos algunas:
- Con el comando table:
El comando table nos muestra la frecuencias de cada dato, así que si el conjunto de datos no es muy grande esta función será suficiente.
Usando la base de datos de 25 lechones destetados:
table(destete25)peso
3.9 6.74 7.26 7.48 7.53 7.67 7.82 8.03 8.32 8.35 8.39 8.48 8.53
1 1 1 1 1 1 1 1 1 1 1 1 1
8.57 8.66 9.48 9.92 10.1 10.45 10.83 10.91 11.03 12.16 12.47 15.8
1 1 1 1 1 1 1 1 1 1 1 1 Se observa que ningun valor se repite ya que cada valor tiene frecuencia 1, es decir que no hay moda.
Usando la base de datos de 100 lechones destetados:
table(destete100$peso)
4.31 5.24 5.69 6.14 6.28 6.33 6.41 6.63 6.65 6.77 6.84 6.87 6.91
1 1 1 1 1 1 1 1 1 1 1 1 1
6.92 6.99 7.09 7.2 7.22 7.27 7.34 7.42 7.52 7.62 7.7 7.81 7.83
1 3 1 1 1 1 1 1 1 1 1 1 1
7.95 7.99 8.09 8.14 8.3 8.45 8.5 8.51 8.52 8.57 8.6 8.62 8.75
1 1 1 1 1 1 1 1 2 2 1 1 1
8.84 8.97 9.02 9.06 9.27 9.28 9.32 9.33 9.34 9.35 9.38 9.63 9.67
1 1 1 1 1 2 1 1 1 1 1 2 1
9.69 9.72 9.74 9.78 9.82 9.92 10.18 10.4 10.41 10.6 10.65 10.8 11.13
1 1 1 1 1 1 3 1 1 1 2 1 1
11.17 11.2 11.38 11.4 11.44 11.5 11.64 11.84 11.88 11.89 11.96 12.19 12.26
1 1 1 1 1 1 1 1 1 1 1 1 1
12.52 13.08 13.18 13.38 13.77 13.88 14.02 14.2 14.32 14.91 14.94 15.06 16.13
1 1 1 1 1 1 1 1 1 1 1 1 1 Se observa que hay 2 modas: 6.99 y 10.18 ambos valores con frecuencia 3.
Aunque aún es factible ver la moda en una base con 100 datos, puede complicarse, por eso se presenta a continuación una segunda forma.
Con table y max:
Cuando hay muchos datos es difícil observar cada frecuencia para determinar cuál es la moda, en esos casos es conveniente utilizar una combinación de table y de max.
El comando table indicará la frecuencia de cada valor, luego al utilizar los corchetes se puede indexar los valores de acuerdo a un criterio, en este caso el criterio es max, con esto se logra que el comando devuelva los valores ue más se repiten sin importar si la distribución es bimodal o incluso si tiene más de dos modas.
Con la base de datos de 100 lechones destados:
table(destete100$peso)[table(destete100$peso) == max(table(destete100$peso))]
6.99 10.18
3 3 Se observa que la distribución es bimodal, los valores que más se repiten son 6.99 y 10.18, ambos con frecuencia 3.
Usando la base de datos de 10,000 lechones destetados:
table(destete10000$peso)[table(destete10000$peso) == max(table(destete10000$peso))]
9.61 10.06 10.87
27 27 27 La distribución tiene tres modas: 9.91, 10.06 y 10.87, con frecuencia 27.
Con esta base de datos de 10,000 lechones destetados queda claro que esta forma es más eficiente que la forma 1 en la que solo se usa el comando table.
- Gráficas
Gráfico de puntos:
También se le llama gráfico de dispersión o scatterplot.
En este gráfico, en el eje X u horizontal se coloca la numeración de los datos, y en el eje Y o vertical se colocan los valores propiamente dichos.
Cada punto es una observación.
plot(destete25$peso)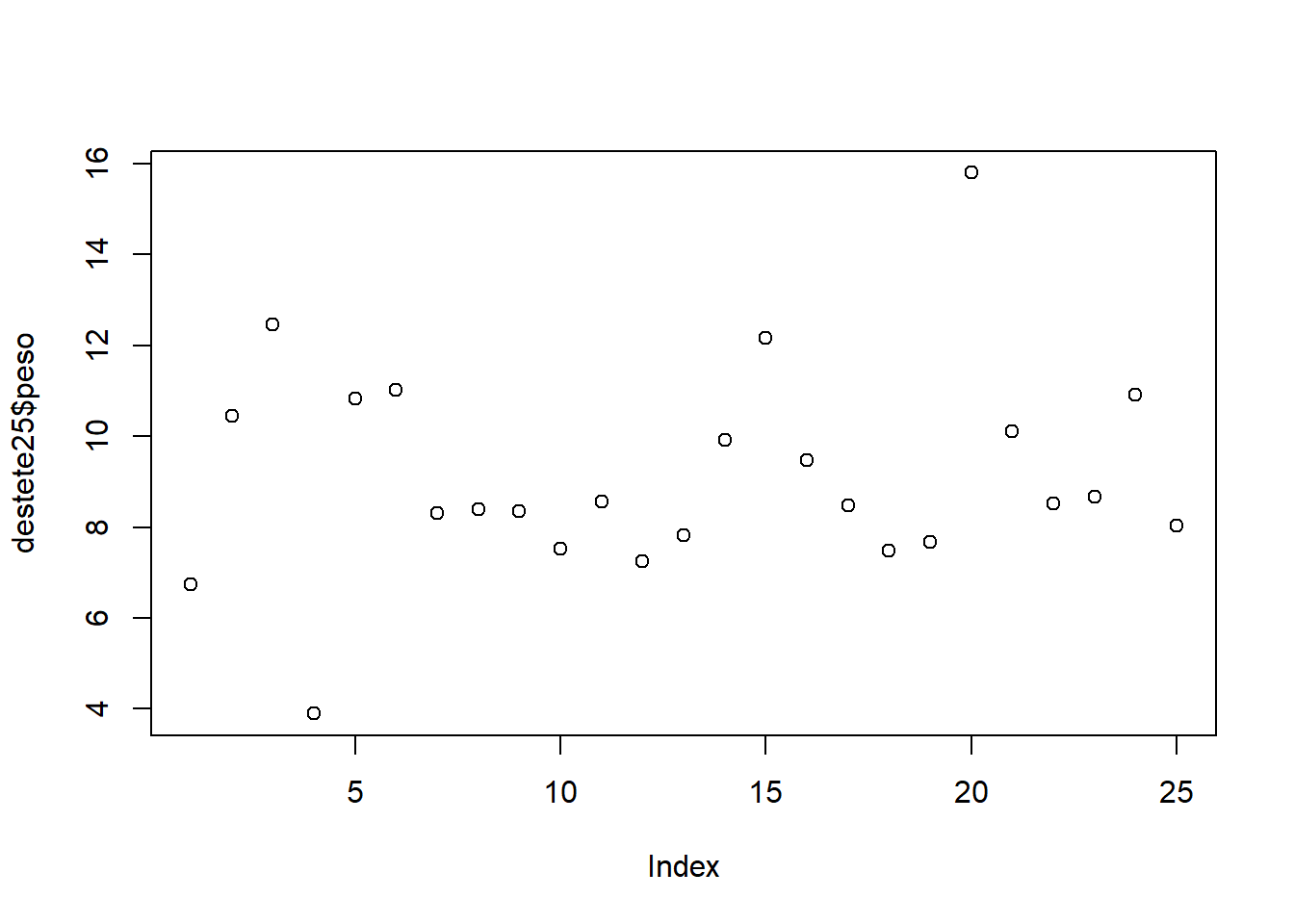
Se puede trazar una línea que represente el promedio
plot(destete25$peso)
abline(h = mean(destete25$peso))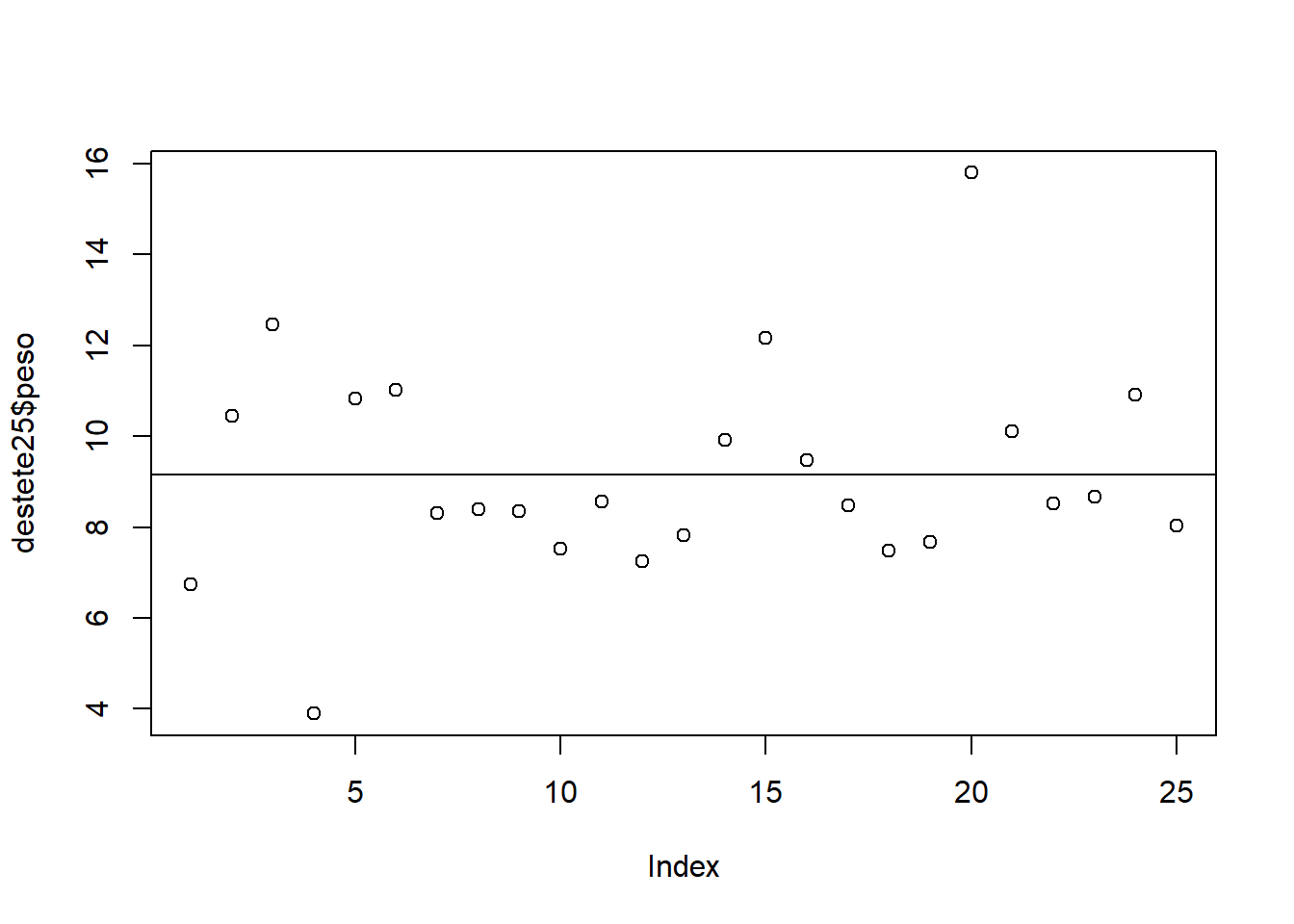
Con esta gráfica se observa que hay 15 valores debajo del promedio y 10 valores arriba del promedio, esto es un indicador de que la distribución no es completamente simétrica. Hay mayor dispersión en los datos que están por encima del promedio que en los datos que están por debajo del promedio, habiendo por encima del promedio unos pocos datos muy altos elevándose así el promedio, esto es relevante ya que el promedio está siendo elevado por unos pocos datos, esto puede significar que el proceso (el crecimiento de los lechones) es inestable, y por tanto propenso a cambios repentinos, pudiéndose presentar en futuros lotes un descenso del promedio si algún evento negativo ocurre en algunos lechones como por ejemplo alguna enfermedad viral, algún factor estresante, o algún fallo en el manejo aunque solo involucre a pocos lechones.
Se puede incluir además de una línea que represente el promedio, una línea que represente la mediana
plot(destete25$peso)
abline(h = mean(destete25$peso), col = "blue")
abline(h = median(destete25$peso), col = "green")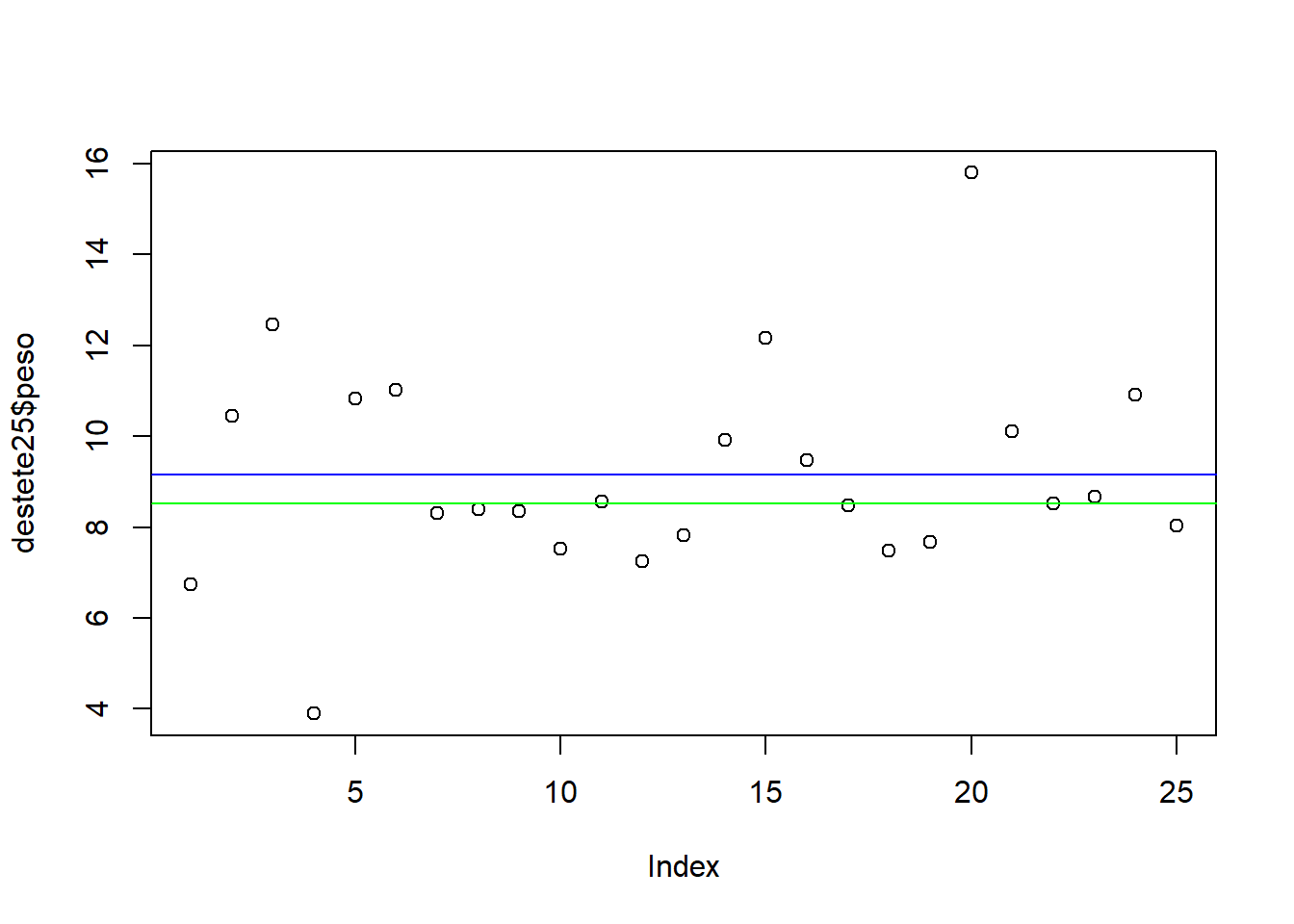
Gráfico de densidad
plot(density(destete25$peso))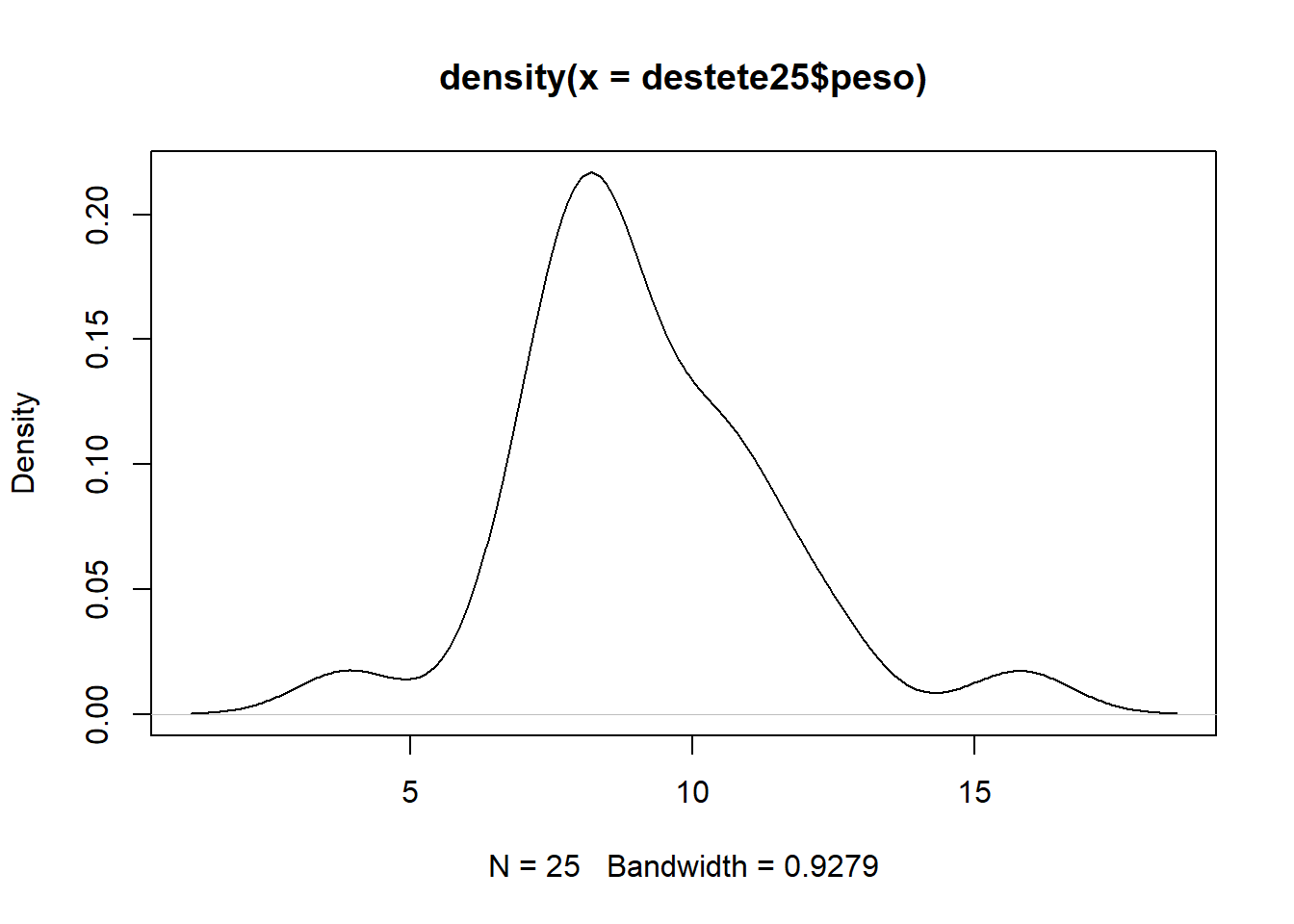
Se le puede agregar una línea con el promedio
plot(density(destete25$peso))
abline(v = mean(destete25$peso), col = "blue")
abline(v = median(destete25$peso), col = "green")
3.4 Medidas de dispersión
El grado de dispersión de los datos numéricos respecto a un valor promedio se llama dispersión o variación de los datos.(Spiegel and Stephens 2009) Aquí se verán 3 medidas de dispersión: Rango, Varianza, Desviación estandar y Coeficiente de variación.
Rango
El rango de un conjunto de números es la diferencia entre el número mayor y el número menor del conjunto.(Spiegel and Stephens 2009)
El intervalo de la muestra se calcula con mucha facilidad, pero tiene la inconveniencia de que se ignora toda la información que existe entre las observaciones más pequeña y más grande. Para tamaños de muestra pequeños, digamos menores o iguales a 10, esta pérdida de información no es demasiado seria en algunas situaciones.(Montgomery, n.d.)
\[\begin{equation}{} R = Xmax - Xmin \end{equation}\]
Varianza
Es el promedio de las desviaciones de las observaciones respecto de su media aritmética, elevadas al cuadrado.(Proaño 2020)
Existe la varianza muestral y la varianza poblacional, la varianza muestral se identifica con el símbolo \(s^2\) y la varianza poblacional se identifica con el símbolo de la letra griega delta en minúscula \(\delta\)
\[\begin{equation}{} s^2 = \frac{\sum_{i=1}^n(x_i-\bar{x})^2}{n-1} \end{equation}\] \[\begin{equation}{} \delta^2 = \frac{\sum_{i=1}^N(x_i-\bar{x})^2}{N} \end{equation}\]
Desviación estandar
Es la raíz cuadrada de la varianza.
También hay una desviación estandar muestral y una desviación estandar poblacional.
\[\begin{equation}{} s^2 = \sqrt \frac{\sum_{i=1}^n(x_i-\bar{x})^2}{n-1} \end{equation}\] \[\begin{equation}{} \delta^2 = \sqrt \frac{\sum_{i=1}^N(x_i-\bar{x})^2}{N} \end{equation}\]
Coeficiente de variación
El coeficiente de variación es la proporción entre la desviación estandar y el promedio. Es decir que es una forma de expresa la variación promedio de los datos respecto al promedio general (tal como lo hace la desviación estandar) pero expresado como una proporción.
Si el resultado se multiplica por 100 obtenemos la variación en porcentaje.
\[\begin{equation}{} CV = \frac{s} {\bar{x}} \end{equation}\] \[\begin{equation}{} \%CV = \frac{s} {\bar{x}} · 100 \end{equation}\]
3.5 Medidas de posición
3.6 Análisis exploratorio
El análisis exploratorio de datos es el proceso para utilizar herramientas estadísticas (como gráicas, medidas de tendencia central y medidas de variación), con la finalidad de investigar conjuntos de datos para comprender sus características importantes.(Triola 2004)